- 刷题日记 - 7
- 452. 用最少数量的箭引爆气球 - 力扣(LeetCode)
- 71. 简化路径 - 力扣(LeetCode)
- 150. 逆波兰表达式求值 - 力扣(LeetCode)
- 224. 基本计算器 - 力扣(LeetCode)
- 141. 环形链表 - 力扣(LeetCode)
- 2. 两数相加 - 力扣(LeetCode)
- 21. 合并两个有序链表 - 力扣(LeetCode)
- 23. 合并 K 个升序链表 - 力扣(LeetCode)
刷题日记 - 7
记录刷题。
难度:中等
区间题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (int[] a, int[] b) -> Integer.compare(a[0], b[0]));
int res = 1;
int len = points.length;
int left = points[0][0];
int right = points[0][1];
int p = 1;
while (p < len) {
int curLeft = points[p][0];
int curRight = points[p][1];
if (curLeft > right) {
res++;
left = curLeft;
right = curRight;
} else {
left = curLeft;
right = Math.min(curRight, right);
}
p++;
}
return res;
}
}
|
区间排序:便于后续处理。
区间合并:需要判断各个区间的并集,更新left right为并集的范围。如果下一个区间与该并集没有重合,表明扎暴后面的气球至少还需要一根针,所以将res++。由于没有并集,所以更新left right为curLeft curRight,再重复上面的操作。
返回的所需要的最少的弓箭数,就是尽可能多地找到哪些涉及区间多的并集。
难度:中等
栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public String simplifyPath(String path) {
String[] dirs = path.split("/");
Deque<String> list = new LinkedList<>();
for (int i = 1; i < dirs.length; i++) {
String dir = dirs[i];
if (dir.equals("..")) {
if (!list.isEmpty()) {
list.pollLast();
}
} else if (!(dir.equals(".") || dir.length() == 0)) {
list.offerLast(dir);
}
}
StringBuilder sb = new StringBuilder();
while (!list.isEmpty()) {
String dir = list.pollFirst();
sb.append("/");
sb.append(dir);
}
if (sb.length() == 0) {
return "/";
}
return sb.toString();
}
}
|
这里使用了双端队列Deque,便于最后将值依次取出。
难度:中等
栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if (token.equals("+")) {
int opNum1 = stack.pop();
int opNum2 = stack.pop();
int res = opNum1 + opNum2;
stack.push(res);
}
else if (token.equals("-")) {
int opNum1 = stack.pop();
int opNum2 = stack.pop();
int res = opNum2 - opNum1;
stack.push(res);
}
else if (token.equals("*")) {
int opNum1 = stack.pop();
int opNum2 = stack.pop();
int res = opNum1 * opNum2;
stack.push(res);
}
else if (token.equals("/")) {
int opNum1 = stack.pop();
int opNum2 = stack.pop();
int res = opNum2 / opNum1;
stack.push(res);
}
else {
stack.push(Integer.parseInt(token));
}
}
return stack.pop();
}
}
|
逆波兰表达式的理解,将操作符放在操作数之后,并通过栈来保存和处理操作数。
注意除法和减法的操作数顺序:opNum2 - opNum1 和 opNum2 / opNum1
难度:困难
栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| class Solution {
public int calculate(String s) {
char[] sChars = s.toCharArray();
int len = s.length();
int INIT = 0;
int HAVE_ONE_NUM = 1;
int HAVE_OP = 2;
int state = INIT;
Stack<Character> chStack = new Stack<>();
Stack<Integer> numStack = new Stack<>();
int p=0;
while(p<len){
if(sChars[p]==' '){
p++;
}
if(p>=len)break;
if(Character.isDigit(sChars[p])){
int[] tmp = findNextInt(sChars,p);
int curNum = tmp[0];
p = tmp[1];
if(state==INIT){
numStack.push(curNum);
state = HAVE_ONE_NUM;
}else if(state==HAVE_OP){
char op = chStack.pop();
if(op=='+'){
int res = numStack.pop()+curNum;
numStack.push(res);
state = HAVE_ONE_NUM;
}else if(op=='-'){
int res = numStack.pop() - curNum;
numStack.push(res);
state = HAVE_ONE_NUM;
}
}
}else if(sChars[p]=='+'||sChars[p]=='-'){
if(state==HAVE_ONE_NUM){
chStack.push(sChars[p]);
state = HAVE_OP;
}else if(state == INIT){
numStack.push(0);
chStack.push('-');
state = HAVE_OP;
}
p++;
}else if(sChars[p]=='('){
state = INIT;
chStack.push(sChars[p]);
p++;
}else if(sChars[p]==')'){
while(p<len&&(sChars[p]==')'&&chStack.peek()=='(')){
chStack.pop();
p++;
}
if(numStack.size()>=2){
int opNum1 = numStack.pop();
int opNum2 = numStack.pop();
char op = chStack.pop();
if(op=='+'){
numStack.push(opNum1+opNum2);
}else if(op=='-'){
numStack.push(opNum2-opNum1);
}
}
state = HAVE_ONE_NUM;
}
}
return numStack.pop();
}
private int[] findNextInt(char[] sChars,int p){
int len = sChars.length;
int curNum = 0;
while(p<len&&Character.isDigit(sChars[p])){
curNum = curNum*10 + (sChars[p] - '0');
p++;
}
int[] res = new int[2];
res[0] = curNum;
res[1] = p;
return res;
}
}
|
能用状态机做主要是因为只有+和-,根据当前的字符和当前的状态进行状态转移:
一个很草的图:
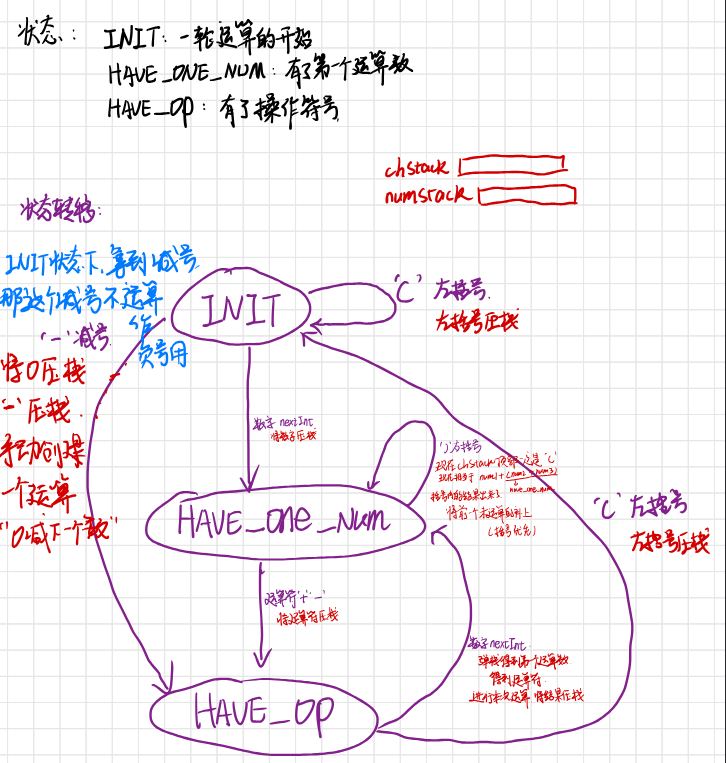
难度:简单
链表 快慢指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
boolean res = false;
while(fast != null){
fast = fast.next;
if(fast == null) break;
fast = fast.next;
slow = slow.next;
if(fast == slow){
res = true;
break;
}
}
return res;
}
}
|
可以利用哈希表来做,用一个指针遍历所有节点,利用哈希表来判断当前节点是否已经访问过(是否有环)。
但是哈希表法空间复杂度太高,最坏情况下要将所有的节点都加入哈希表中。
所以更好还是采用快慢指针的做法,如果有环,则快慢指针必定会相遇。
难度:中等
链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode p = l1;
ListNode q = l2;
ListNode dummy = new ListNode(-1);
ListNode t = dummy;
int carry = 0;
while(p != null && q != null){
int val = p.val + q.val + carry;
carry = (val >= 10) ? 1 : 0;
val = (val >= 10) ? val % 10 : val;
ListNode tmp = new ListNode(val);
t.next = tmp;
t = t.next;
p = p.next;
q = q.next;
}
ListNode remainNode = (p == null) ? q : p;
while(remainNode != null){
int val = carry + remainNode.val;
carry = (val >= 10) ? 1 : 0;
val = (val >= 10) ? val % 10 : val;
ListNode tmp = new ListNode(val);
t.next = tmp;
t = t.next;
remainNode = remainNode.next;
}
if(carry != 0){
t.next = new ListNode(carry);
}
return dummy.next;
}
}
|
主要注意四个点:使用dummy节点简化处理 处理进位问题 处理不同长度的链表 处理最后的进位
难度:简单
链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode p = list1;
ListNode q = list2;
ListNode dummy = new ListNode(-1);
ListNode t = dummy;
while(p != null && q != null){
if(p.val >= q.val){
t.next = q;
t = t.next;
q = q.next;
} else {
t.next = p;
t = t.next;
p = p.next;
}
}
t.next = (p == null) ? q : p;
return dummy.next;
}
}
|
难度:困难
链表 最小堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public ListNode mergeKLists(ListNode[] lists) {
PriorityQueue<ListNode> pq = new PriorityQueue<>(
(ListNode a, ListNode b) -> (a.val - b.val)
);
for(ListNode head : lists){
if(head == null) continue;
pq.offer(head);
}
ListNode dummy = new ListNode(-1);
ListNode t = dummy;
while(!pq.isEmpty()){
t.next = pq.poll();
t = t.next;
if(t.next == null) continue;
pq.offer(t.next);
}
return dummy.next;
}
}
|
可以利用第21题,可以将K个升序链表两两合并。
但是最优解是利用最小堆数据结构,每次从堆中取出值最小的节点。
