^-^
I am who I am.
回溯 - Backtracking
最近更新：2025-10-20   |   字数总计：3.7k   |   阅读估时：17分钟   |   阅读量：次
  1. 基础算法 - 回溯
    1. 相关题目
      1. 46. 全排列 - 力扣（LeetCode）
      2. 47. 全排列 II - 力扣（LeetCode）
      3. 78. 子集 - 力扣（LeetCode）
        1. 动态规划
        2. 回溯
      4. 17. 电话号码的字母组合 - 力扣（LeetCode）
      5. 39. 组合总和 - 力扣（LeetCode）
      6. 22. 括号生成 - 力扣（LeetCode）
      7. 79. 单词搜索 - 力扣（LeetCode）
      8. 131. 分割回文串 - 力扣（LeetCode）
      9. 51. N 皇后 - 力扣（LeetCode）

基础算法 - 回溯

回溯（Backtracking）作为一种重要的算法设计技术，在解决组合问题、排列问题以及搜索问题中广泛应用。其核心思想是通过试探和撤销的方式，在搜索过程中找到所有可能的解决方案。

回溯算法的主要特点包括：

  • 递归：回溯算法通常采用递归方式实现，通过递归函数进行问题的求解。
  • 试探：在每一步中，尝试不同的选择，进入下一步递归。
  • 撤销：当当前选择不满足问题的要求时，撤销该选择并尝试其他可能的选择。

回溯算法适用于解决那些具有多个步骤和多个选择的问题，例如全排列、组合、子集、数独、八皇后等问题。其时间复杂度通常较高，但可以通过剪枝等优化方法提高效率。

回溯问题都可以通过画树图的方式理思路

相关题目

46. 全排列 - 力扣（LeetCode）

难度：中等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    // res为最终返回的答案
    public List<List<Integer>> res = new ArrayList<>();
    // 全排列
    public List<List<Integer>> permute(int []nums){
        // 数组的长度
        int num = nums.length;
        // isUsed 记录对应的元素是否被使用过 状态变量
        // 初始值为false
        boolean[] isUsed = new boolean[num];
        // 记录每一次排列的临时数组
        List<Integer> tmp = new ArrayList<>();
        // index记录当前临时数组中的元素个数
        int index = 0;
        dfs(nums,num,index,isUsed,tmp);
        return res;
    }

    void dfs(int[] nums, int num, int index, boolean[] isUsed, List<Integer> tmp){
        // 当tmp数组中满了的时候，就直接退出函数（出栈）
        if(index==num){
//            res.add(tmp);  这样是错误的，因为这样我添加的就是tmp的引用而不是tmp的拷贝
            res.add(new ArrayList<>(tmp));
            return;
        }
        for(int i=0;i<num;i++){
            // 如果访问的当前的这个元素没有被使用过，那么就将其加入tmp，并且还要更新状态
            if(!isUsed[i]){
                tmp.add(nums[i]);
                index++;
                isUsed[i] = true;
                // 然后深度优先搜索了
                dfs(nums,num,index,isUsed,tmp);
                // dfs出栈之后，就需要将状态更新
                index --;
                isUsed[i] = false;
                tmp.remove(tmp.size()-1);
            }
        }
    }
}

主要涉及到栈的深度优先遍历，回溯所需要的depth（index）、状态记录（isUsed）…

还要注意到java的参数引用传递

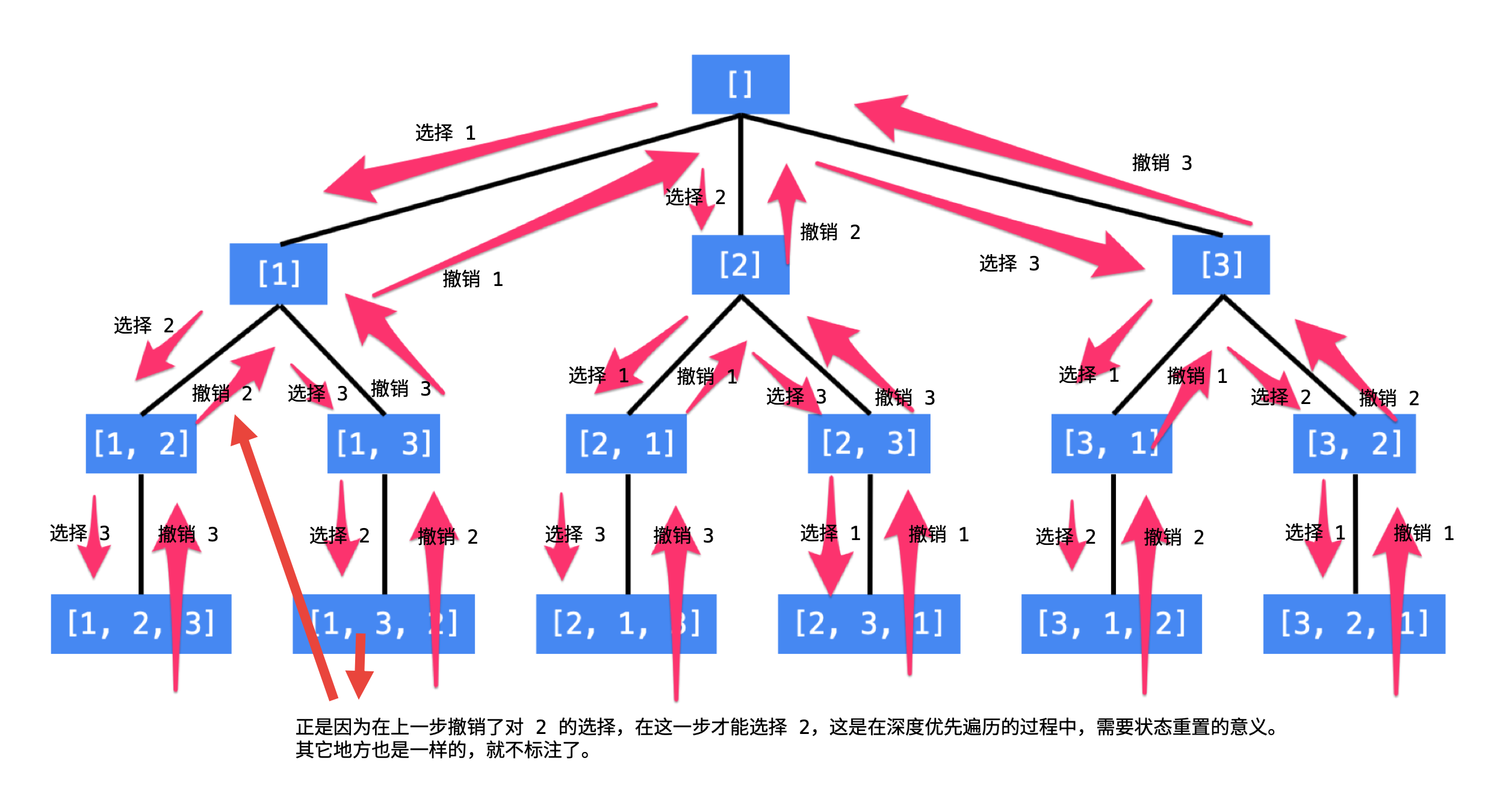
image.png

47. 全排列 II - 力扣（LeetCode）

难度：中等

画数图会发现，只要在每一层保证重复的元素只用一次即可。

可以用哈希表来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> tmp = new ArrayList<>();
        int[] state = new int[nums.length];
        int count = 0;
		dfs(res,tmp,nums,state,0);
        return res;
    }
    
    private void dfs(List<List<Integer>> res,List<Integer> tmp,int[] nums,int[] state,int count){
        HashSet<Integer> map = new HashSet<>();  // 记录在前一个节点下 当前层出现过哪些值
        if(count==nums.length){
            res.add(new ArrayList<>(tmp));
        }
        for(int i=0;i<nums.length;i++){
            if(state[i]==0){
                if(map.contains(nums[i])) continue; // 剪枝
                else map.add(nums[i]);
                state[i]=1;
                tmp.add(nums[i]);
                dfs(res,tmp,nums,state,count+1);
                tmp.remove(count);
                state[i]=0;
            }
        }
    }
}

78. 子集 - 力扣（LeetCode）

难度：中等

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    // 子集
    // 根据子集的特点，可以把它看作一种动态规划
    public List<List<Integer>> subsets(int[] nums){
        // 先将空集加入
        res.add(new ArrayList<>());
        // nums的长度
        int num = nums.length;
        for(int i = 0; i<num; i++){
            int size = res.size();
            System.out.println(size);
            System.out.println(res);
            for(int j = 0; j<size; j++){
                // 获取之前的子集，新的子集 = 之前的子集 + 新元素
                // dp[i] = dp[i-1] + new
                List<Integer> new_t = new ArrayList<>(res.get(j));
                new_t.add(nums[i]);
                res.add(new ArrayList<>(new_t));
            }
        }
        return res;
    }
}

使用了动态规划的思想，如果当前数组为[1,2,3]，dp[0]初始状态为空集，dp[1]为[]加上[1]，

dp[2] = dp[1] + new，而这个new就等于以前的dp[1]中的所有子集加上这个新的2。

回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    List<Integer> t = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }

    public void dfs(int cur, int[] nums) {
        // 访问到了最后一个位置，将t数组中的元素加入
        if (cur == nums.length) {
            ans.add(new ArrayList<Integer>(t));
            return;
        }
        // 将当前元素加入 进行遍历
        t.add(nums[cur]);
        dfs(cur + 1, nums);
        // 将当前元素移除 进行遍历
        t.remove(t.size() - 1);
        dfs(cur + 1, nums)
    }
}

因为每一个元素其实有两个状态，被选中或者未被选中，我们依次dfs即可。

可以想象成一个二叉树，每一层代表每一个元素，左子树代表选中，右子树代表未选中，从根节点到叶子节点的路径就为一个子集。

17. 电话号码的字母组合 - 力扣（LeetCode）

难度：中等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public List<String> letterCombinations(String digits) {
        // 初始化 map
        HashMap<Character,String> map = new HashMap<Character,String>();
        map.put('2', "abc");
        map.put('3', "def");
        map.put('4', "ghi");
        map.put('5', "jkl");
        map.put('6', "mno");
        map.put('7', "pqrs");
        map.put('8', "tuv");
        map.put('9', "wxyz");
        // res是要返回的结果,初始值为空
        ArrayList<String> res = new ArrayList<>();

        if(digits.equals("")){
            return res;
        }
    
        // StringBuffer 数据结构对于String的处理提供的接口更加多
        dfs(res,map,digits,0,new StringBuffer());
        return res;
    }

    public void dfs(List<String> res,HashMap<Character,String> map,String digits, int index, StringBuffer tmp){
        // index代表当前tmp中有多少个字母了
        if(index == digits.length()){
            // 当字母数量足够了的时候，就需要记录这个字母组合，也就是tmp
            res.add(tmp.toString());
            return;
        }
        // 根据index取出需要的digit
        char digit = digits.charAt(index);
        // 从map中获得数字对应的letters
        String letters = map.get(digit);
        // 获得letters的长度，进行dfs遍历
        int letterLen = letters.length();
        // 遍历过程
        for(int i=0;i<letterLen;i++){
            // 将字母加入临时组合tmp
            tmp.append(letters.charAt(i));
            // 第index位的字母已经被选中，通过dfs往更深的地方寻找目标
            dfs(res,map,digits,index+1,tmp);
            // 回溯，退回之后要将第index位的字符给弹出（状态改变）
            tmp.deleteCharAt(index);
        }
    }

回溯的精髓就在于 回退之后的状态改变

也就是递归之后需要做和递归之前相反的事情

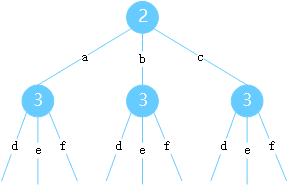
算法过程.png

39. 组合总和 - 力扣（LeetCode）

难度：中等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<Integer> tmp = new ArrayList<>();
        for(int i = 0;i<candidates.length;i++){
            tmp.add(candidates[i]);
            dfs(candidates,target,tmp, candidates[i],i);
            tmp.remove(tmp.size()-1);
        }
        return res;
    }

    private void dfs(int[] candidates, int target,List<Integer> tmp,int sum,int pos){   // 这个pos是去重的关键
        if(sum==target){
            res.add(new ArrayList<>(tmp));
            return;
        }
        if(sum>target){
            return;
        }
        
        for(int i=pos;i<candidates.length;i++){
            tmp.add(candidates[i]);
            dfs(candidates,target,tmp,sum+candidates[i],i);
            tmp.remove(tmp.size()-1);
        }
    }
}

题目告诉了给出的nums数组中的元素是不重复的（而且还是按照从小到大的顺序的）

未考虑去重：

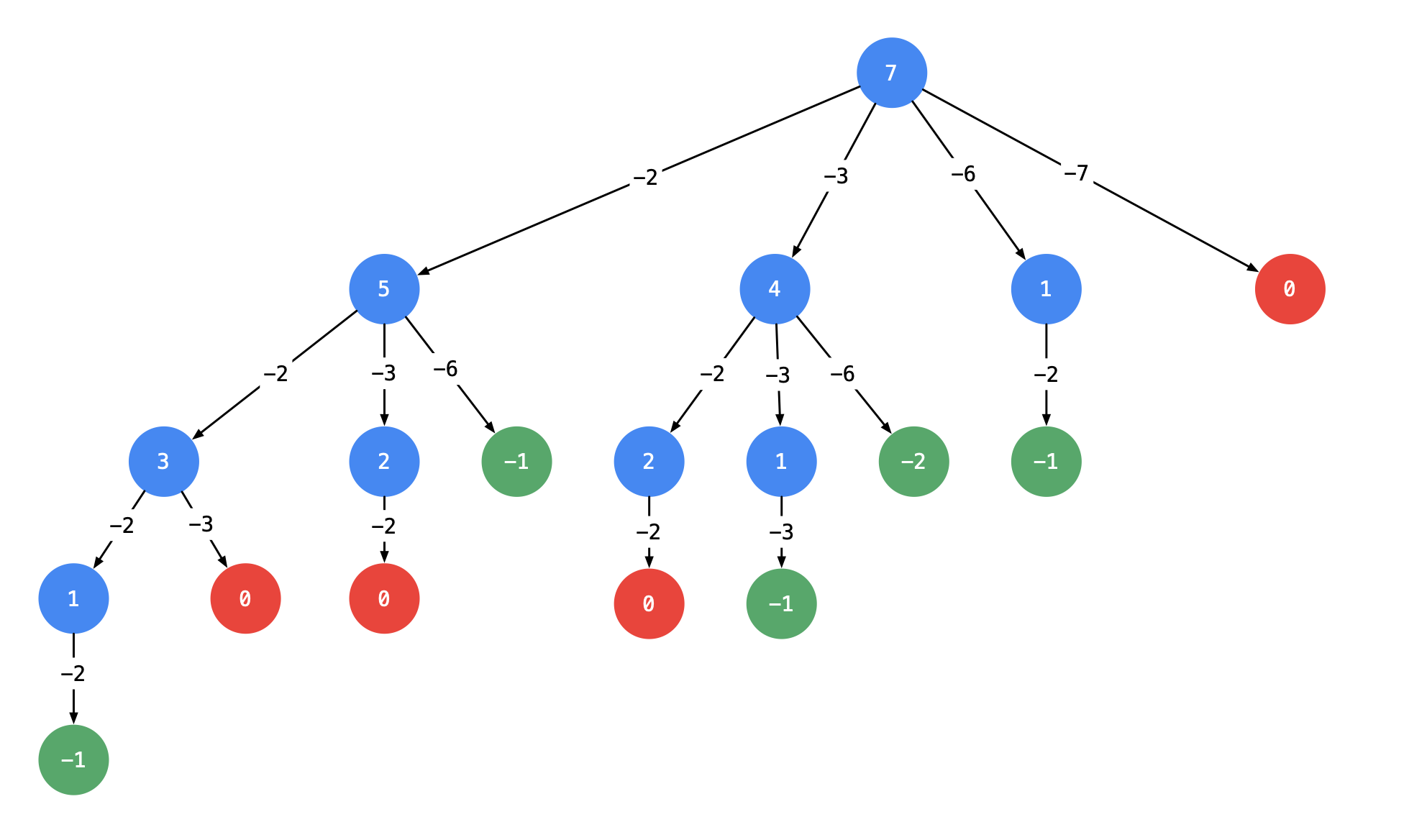
1598091943-hZjibJ-file_1598091940241

考虑去重:

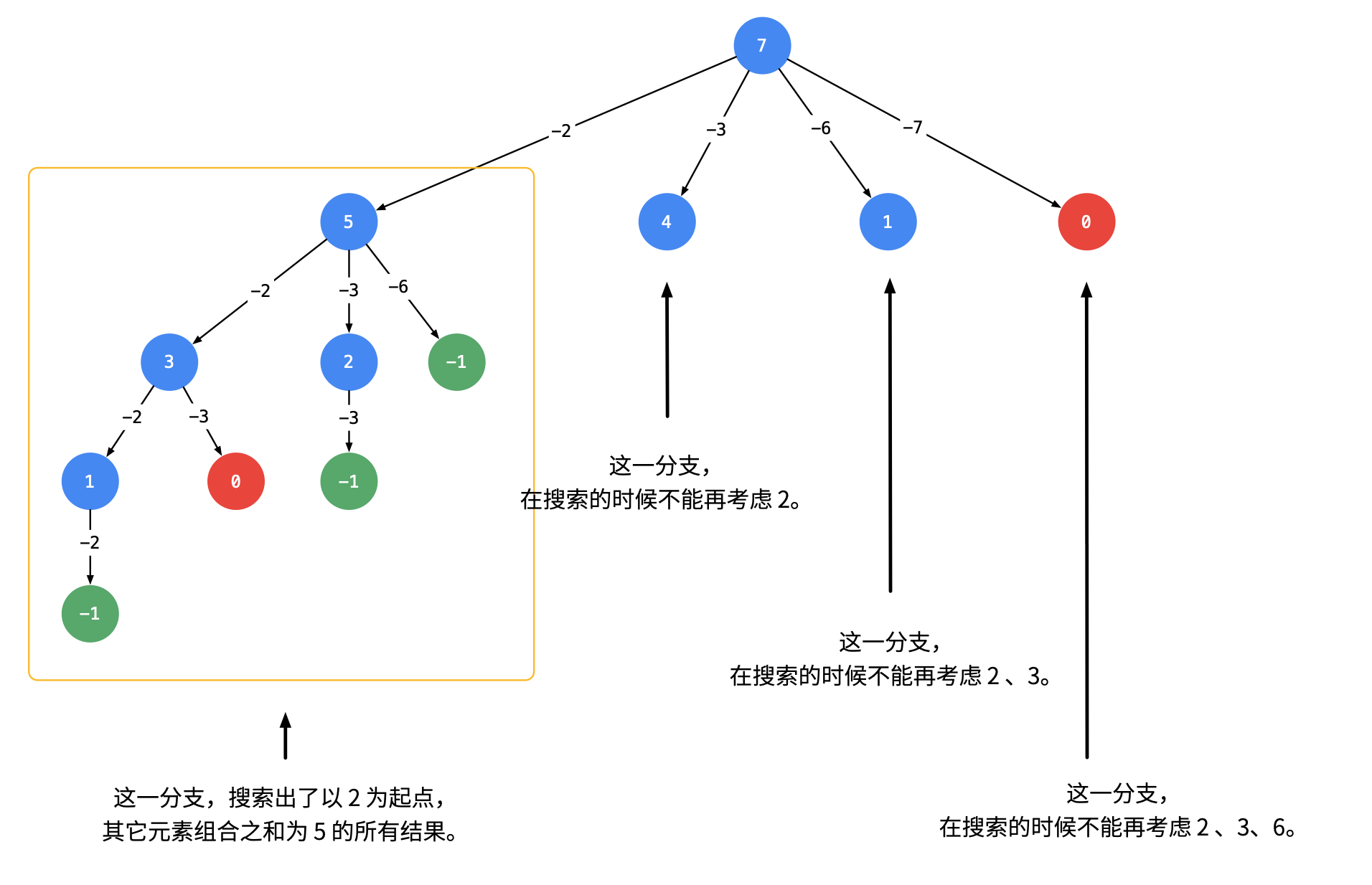
1598091943-GPoHAJ-file_1598091940246

22. 括号生成 - 力扣（LeetCode）

难度：中等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    List<String> res = new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        StringBuffer sb = new StringBuffer();
        dfs(n,n,sb);
        return res;
    }

    private void dfs(int left,int right,StringBuffer sb){
        if(left==0&&right==0){
            res.add(sb.toString());
            return;
        }
        if(left>0){
            sb.append('(');
            dfs(left-1,right,sb);
            sb.deleteCharAt(sb.length()-1);
        }
        if(left<right){   // 这里要加以限制一下（括号合法）
            sb.append(')');
            dfs(left,right-1,sb);
            sb.deleteCharAt(sb.length()-1);
        }
    }
}

可以想象成二叉树，根节点往左拐就是增加一个左括号，往右拐增加一个右括号，找到满足合法括号的路径。

在这里sb相当于栈。

79. 单词搜索 - 力扣（LeetCode）

难度：中等

二维的dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution_exist_redo {
    boolean res = false;
    int[][] dr = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};  // 代表四个方向
    boolean[][] state;

    public boolean exist(char[][] board, String word) {
        state = new boolean[board.length][board[0].length];
        int idx = 0;
        int needChar = word.charAt(idx);  // 当前需要的字符串
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (board[i][j] == needChar) {
                    state[i][j] = true;
                    dfs(board, word, idx + 1, i, j);  // 以这个为基准往四周dfs寻找
                    state[i][j] = false;
                    if(res) return true;
                }
            }
        }
        return res;
    }

    private void dfs(char[][] board, String word, int idx, int x, int y) {
        if (idx == word.length()) {
            res = true;
            return;
        }
        for (int i = 0; i < 4; i++) {  // for遍历四个方向
            // 如果res=true，表明已经找到了提前结束dfs
            if (res) return;
            // 新位置
            int nextX = x + dr[i][0];
            int nextY = y + dr[i][1];
            // 新位置是否越界，新位置是否访问过，新位置的值是否是想要的
            if (nextX < 0 || nextX >= board.length)
                continue;
            if (nextY < 0 || nextY >= board[0].length)
                continue;
            if (state[nextX][nextY])
                continue;
            if (board[nextX][nextY] != word.charAt(idx))
                continue;
            state[nextX][nextY] = true;
            dfs(board, word, idx + 1, nextX, nextY);
            state[nextX][nextY] = false;
        }
    }
}

但是dfs回溯的思想是一样的。

131. 分割回文串 - 力扣（LeetCode）

难度：中等（较难）

要先理解怎么判断回文字符串（动态规划），然后回溯寻找所有可能的分割方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    List<List<String>> res;
    boolean[][] dp;
    List<String> tmp;

    public List<List<String>> partition(String s) {
        // 初始化
        res = new ArrayList<>();
        tmp = new ArrayList<>();
        int len = s.length();
        dp = new boolean[len][len]; // dp[i][j]表示字符串s[i]..s[j]是不是回文字符串
        // 初始化dp，dp[i][j], 当j>=i的时候，也就是dp的左下角都是true，这样才不影响后续的dp
        for (int i = 0; i < len; i++)
            Arrays.fill(dp[i], true);
        // 动态规划  这里一定要倒着来，因为dp[i]计算需要dp[i+1]
        // j 正着来，因为dp[i][j]依赖与dp[i+1][j-1]，j-1
        for (int i = len - 1; i >= 0; i--) {
            for (int j = i + 1; j < len; j++) {
                dp[i][j] = dp[i + 1][j - 1] && (s.charAt(i) == s.charAt(j));
            }
        }
        dfs(s,0);
        return res;
    }

    private void dfs(String s, int cur) {
        if (cur == s.length()) {
            res.add(new ArrayList<>(tmp));
            return;
        }
        for (int i = cur; i < s.length(); i++) {
            if (dp[cur][i]) {
                tmp.add(s.substring(cur,i+1));
                dfs(s,i+1);  // 进入下一个dfs的是i+1,不是cur
                tmp.remove(tmp.size()-1);
            }
        }
    }
}

动态规划 + 回溯

核心思路

  1. 动态规划预处理：首先使用动态规划（DP）来预处理字符串 s，确定每个子串是否为回文。这部分预处理将帮助我们在回溯时快速判断子串是否为回文，从而减少不必要的重复计算。
  2. 回溯（DFS）：然后使用回溯（深度优先搜索，DFS）来尝试所有可能的分割方式。每当发现一个合法的回文子串时，就递归地继续分割剩余的字符串，直到处理完整个字符串。

以aabb为例：

1
2
3
4
5
6
7
8
9
10
11
               ""
             /     \
           "a"     "aa"
          /   \       \
        "a"   "ab"    "b"
        / \      (不合法) \
      "b" "bb"           "b"
      /     \            (空)
   "b"     "b" 
   /         (空)
(空)

51. N 皇后 - 力扣（LeetCode）

难度：困难

掌握了dfs的核心之后这个题就变得非常简单了，本题最复杂的点就是如何对访问过的点做标记。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
class Solution {
    // 用数组来记录位置
    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    // 记录状态，记录每一个格子被多少个皇后锁定了
    public List<List<String>> solveNQueens(int n) {
        // 0 表示没有被皇后锁定，表明下一个皇后可以放置在这个位置上
        // 初始state数组均为0
        int[][] state = new int[n][n];
        dfs(0, state);
        // 答案都存在ans数组里面，但是题目要求我们给出的是字符串...所以我们需要加上这一段,旨在将数组类型的答案转换为字符串List
        List<List<String>> res = new ArrayList<>();
        for (int i = 0; i < ans.size(); i++) {
            path = ans.get(i);
            List<String> tmp = new ArrayList<>();
            for (int j = 0; j < n; j++) {
                StringBuffer stringBuffer = new StringBuffer();
                int pos = path.get(j);
                for (int k = 0; k < n; k++) {
                    if (k == pos) {
                        stringBuffer.append('Q');
                    } else {
                        stringBuffer.append('.');
                    }
                }
                tmp.add(stringBuffer.toString());
            }
            res.add(new ArrayList<>(tmp));
        }
        return res;
    }

    // 如果皇后放在了i，j这个位置，那么需要在state上做一些标记，比如说某一些格子会被攻击
    private void mark(int i, int j, int[][] state) {
        int n = state.length;
        // 注意这样的话state[i][j]就会+4
        for (int k = 0; k < n; k++) {
            // 每一行需要被标记
            state[k][j]++;
            // 每一列也需要被标记
            state[i][k]++;
        }
        // 斜着的
        for (int k = -n + 1; k < n; k++) {
            // i，j同+k，为 \
            if ((0 <= i + k) && (0 <= j + k) && (i + k < n) && (j + k < n)) {
                state[i + k][j + k]++;
            }
            // i,j 异号 k,为/
            if ((0 <= i - k) && (0 <= j + k) && (i - k < n) && (j + k < n)) {
                state[i - k][j + k]++;
            }
        }
    }

    // 对应反相减就可以了
    private void unMark(int i, int j, int[][] state) {
        int n = state.length;
        for (int k = 0; k < n; k++) {
            state[k][j]--;
            state[i][k]--;
        }
        for (int k = -n + 1; k < n; k++) {
            if ((0 <= i + k) && (0 <= j + k) && (i + k < n) && (j + k < n)) {
                state[i + k][j + k]--;
            }
            if ((0 <= i - k) && (0 <= j + k) && (i - k < n) && (j + k < n)) {
                state[i - k][j + k]--;
            }
        }
    }

    private void dfs(int cur, int[][] state) {
        int n = state.length;
        // cur代表这一次的dfs是寻找第cur个皇后的位置的
        // 如果cur等于n，代表所有的皇后都找到了对应的位置了，那么可以返回了
        if (cur == n) {
            ans.add(new ArrayList<>(path));
            return;
        }
        // 遍历每一个位置，尝试每一个位置
        // 经过思考，其实不必要遍历每一个位置，因为N皇后的第一个肯定是在第一行的，第二个肯定是在第二行的....
        // 所以我们就根据cur的值，确定在哪一行进行遍历就可以了(cur可以作为行的索引)
        for (int i = 0; i < n; i++) {
            // 如果有位置的话，就搜索下一个
            if (state[cur][i] == 0) {
                // 先标记
                mark(cur, i, state);
                // tmp中最多有n-1个元素，分别代表每一行的皇后对应的位置
                path.add(i);
                dfs(cur + 1, state);
                // 弹出
                path.remove(path.size() - 1);
                // 清楚标记
                unMark(cur, i, state);
            }
        }
    }
}

和前面的回溯题没什么不同，就是标记元素的方式改变了。Mark()与UnMark()

2024-06-10 该篇文章被 jay1an 打上标签: 基础算法 回溯 归为分类: 基础算法

上一篇：栈 - Stack 下一篇：滑动窗口 - Sliding Window
© 1949-2025 Jay1an
从头努力也坎坷 本站由Hexo驱动｜使用Hexo-theme-A4主题