^-^
I am who I am.
双指针 - Two Pointers
最近更新：2025-10-20   |   字数总计：2.2k   |   阅读估时：9分钟   |   阅读量：次
  1. 基础算法 - 双指针
    1. 相关题目
      1. 283. 移动零 - 力扣（LeetCode）
      2. 11. 盛最多水的容器 - 力扣（LeetCode）
        1. 暴力解法：
        2. 双指针
      3. 15. 三数之和 - 力扣（LeetCode）
      4. 42. 接雨水 - 力扣（LeetCode）
        1. 方法1 - 按行求
        2. 方法2 - 按列求
        3. 方法3 - DP
        4. 方法4 - 双指针

基础算法 - 双指针

双指针（Two Pointers）是一种常见的算法技巧，通常用于解决数组或链表中的问题。它的核心思想是使用两个指针在给定条件下同时移动，以解决问题或优化算法性能。

主要特点

  • 并行移动：双指针通常会从数组或链表的两端开始，并以不同的速度向中间移动，直到两个指针相遇或交叉。
  • 降低时间复杂度：通过使用双指针，可以在不增加空间复杂度的情况下，降低问题的时间复杂度，通常优于暴力求解方法。
  • 适用场景：适合解决排序数组的查找问题、链表中的环检测、数组或字符串的滑动窗口问题等。

相关题目

283. 移动零 - 力扣（LeetCode）

难度：简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public void moveZeroes(int[] nums) {
        int len = nums.length;
        int nonZero = 0; // 记录下一个非0元素应该放置的位置
        
        // 遍历数组，将非0元素依次放置到nonZero位置上
        for (int i = 0; i < len; i++) {
            if (nums[i] != 0) {
                nums[nonZero++] = nums[i];
            }
        }
        
        // 将nonZero之后的位置都置为0
        while (nonZero < len) {
            nums[nonZero++] = 0;
        }
    }
}

11. 盛最多水的容器 - 力扣（LeetCode）

难度：中等

暴力解法：

这是最朴素的暴力解法，计算出每一个可能的结果然后进行比较，当然是一定会超时的，时间复杂度为n^2^。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxArea(int[] height){
        int res = Integer.MIN_VALUE;
        // len>=2
        int len = height.length;
        for(int i=0;i<len-1;i++){
            for(int j=i+1;j<len;j++){
                // w代表宽度，h代表高度
                int w = j - i;
                int h = Math.min(height[i],height[j]);
                res = Math.max(h*w,res);
            }
        }
        return res;
    }
}

双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
        // 关键的一点：让left和right之间收缩！
        // 如果让更高的那一端收缩，那么面积一定会减小；但是如果让短的那一端收缩，那么面积可能会增大！！！
        public int maxArea(int[] height){
        int res = Integer.MIN_VALUE;
        int left = 0;
        int right = height.length-1;
        while(left<right) {
            int w = right - left;
            if (height[left] < height[right])
                res = Math.max(res, height[left++] * w);
            else
                res = Math.max(res, height[right--] * w);
        }
        return res;
    }
}

与暴力解法相比，双指针解法没有计算那些根本没有意义的面积（比如说哪些让更高的一端收缩的面积），双指针更关注于可能得更大值。

15. 三数之和 - 力扣（LeetCode）

如果要暴力破解的话，时间复杂度应该为n^3^，而且还要去重的操作，非常繁琐，肯定会超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    // 注意：只是i!=j!=k而已，不是nums[i]!=nums[j]!=nums[k]
	// 每一个元素只能用一次
	// 但是每组之间三数是不可以相同的（如何去重是关键）
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        // 首先排序
        Arrays.sort(nums);
        int len = nums.length;
        int cur = Integer.MAX_VALUE;
        for (int i = 0; i < len - 2; i++) {
            // 这里的cur代表上一个满足要求的三数中的第一个数
            // 如果nums[i]与cur相同的话，后面会产生相同的答案，故要跳过 ⭐ 去重第一步
            if (cur == nums[i]) continue;
            cur = nums[i];
            // 因为是排过序的，如果cur已经>0，那么后面的都 >cur，一定不满足条件，可以直接break ⭐ 剪枝
            if (cur > 0) break;
            // ⭐ 双指针
            int head = i + 1;
            int tail = len - 1;
            while (head < tail) {
                if (cur + nums[head] + nums[tail] == 0) {
                    // 将答案记录至res
                    List<Integer> tmp = new ArrayList<>();
                    tmp.add(cur);
                    tmp.add(nums[head]);
                    tmp.add(nums[tail]);
                    res.add(new ArrayList<>(tmp));
                    // 将head和tail指针移至可能出现重复的字符串中的最后一个字符   ⭐ 去重第二步
                    while (head < tail && nums[head] == nums[head + 1])
                        head++;
                    while (head < tail && nums[tail] == nums[tail - 1])
                        tail--;
                    // 使得head和tail指针指向与之前不同的值
                    head++;
                    tail--;
                } else if (cur + nums[head] + nums[tail] < 0) {
                    // 由于cur<=nums[head]<=nums[tail] 且nums数组已经排过序了
                    // head++使得和增加，tail--使得和减少
                    head++;
                } else {
                    tail--;
                }
                // 当head==tail时，以cur为第一个值的所有满足要求的条件已经找完了
                // 应该以下一个cur去寻找了
            }
        }
        return res;
    }
}

42. 接雨水 - 力扣（LeetCode）

方法1 - 按行求

利用雨水一定在凹槽里的特点 ，又根据层数计算雨水，将多层分解为多个单层，单层的逻辑很简单。

这样的时间复杂度为 n*(max(height))

如果max(height)很大，那么很容易超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int trap(int[] height) {
    int sum = 0;
    int max = getMax(height);//找到最大的高度，以便遍历。
    for (int i = 1; i <= max; i++) {  // i表示层数，一层一层地求雨水
        boolean isStart = false; //标记是否开始更新 temp
        int temp_sum = 0;
        for (int j = 0; j < height.length; j++) {
            if (isStart && height[j] < i) {
                temp_sum++;
            }
            if (height[j] >= i) { // 遇到比当前高的柱子为界
                sum = sum + temp_sum;
                temp_sum = 0;
                isStart = true;
            }
        }
    }
    return sum;
}
private int getMax(int[] height) {
		int max = 0;
		for (int i = 0; i < height.length; i++) {
			if (height[i] > max) {
				max = height[i];
			}
		}
		return max;
}

作者：windliang
链接：https://leetcode.cn/problems/trapping-rain-water/solutions/9112/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-8/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

方法2 - 按列求

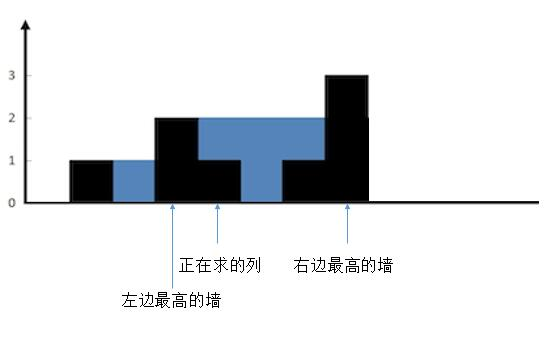
按列求是比较容易想到的方法。

关键思路：如果要求某一列的雨水，需要考虑哪些呢？ – > 左边最高的墙、右边最高的墙、该列的墙的高度，雨水为 = max(min(left,right) - cur,0)

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int trap(int[] height) {
        int res = 0;
        // 根据题目要求 len>=3
        int len = height.length;
        // 求第 2列 到 len-1列的雨水， 端点的两个不用考虑
        for(int i=1;i<len-1;i++){
            int cur = height[i];
            int leftMax = 0;
            int rightMax = 0;
            // 寻找该列左边所有列的最大值
            for(int l=i-1;l>=0;l--)
                leftMax = Math.max(leftMax,height[l]);
            // 右边最大值
            for(int r=i+1;r<len;r++)
                rightMax = Math.max(rightMax,height[r]);
            // 关键：求的该列的雨水
            int low = Math.min(leftMax,rightMax);
            res+=Math.max(low-cur,0);
        }
        return res;
    }
}

这个思路简单，代码简洁，但是时间复杂度稍高n^2^

因为对于每一列，我们都需要重新向左向右遍历最大值。

方法3 - DP

在上一个方法中，我们求leftMax和rightMax的时候很多元素被重复遍历了很多次，造成了时间复杂度稍高。

那么我们就可以使用记忆化搜索的方法来优化求leftMax和rightMax，也就是使用动态规划的方法优化（空间换时间）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int trap(int[] height){
        int res = 0;
        int len = height.length;
        // 记忆化搜索 (动态规划) 空间换时间
        // leftMax[i]代表在第i列以左，最高的列有多高
        // rightMax[i]代表在第i列以右，最高的列有多高
        // 状态更新方程为 ： leftMax[i] = max(leftMax[i-1],height[i-1])
        int[] leftMax = new int[len];
        // rightMax[i] = max(rightMax[i+1],height[i+1])  这个要反着来
        int[] rightMax = new int[len];
        // 所以我们先遍历一遍，将数据记录在dp数组中
        for(int i=1;i<len-1;i++){
            // i: 1 -> len-2
            leftMax[i] = Math.max(leftMax[i-1],height[i-1]);
            // k: len-2 -> 1
            int k = len-1-i;
            rightMax[k] = Math.max(rightMax[k+1],height[k+1]);
        }
        // 接下来leftMax和rightMax就可以在O(1)时间复杂度下获得了
        // 以下的逻辑还是按列求雨水
        for(int i=1;i<len-1;i++){
            int cur = height[i];
            int low = Math.min(leftMax[i],rightMax[i]);
            res+=Math.max(low-cur,0);
        }
        return res;
    }
}

注意，求rightMax[]的时候需要反着来。

这下子时间复杂度为O(n)，但是空间复杂度上去了。

方法4 - 双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int trap_redo(int[] height){
        int res = 0;
        int left = 1;
        int right = height.length-2;
    
        int leftMax = height[left-1];
        int rightMax = height[right+1];
    
        while(left<=right){
            if(leftMax<rightMax){
                res+=Math.max(leftMax-height[left],0);
                leftMax = Math.max(leftMax,height[left]);
                left++;
            }else{
                res += Math.max(rightMax-height[right],0);
                rightMax = Math.max(rightMax,height[right]);
                right--;
            }
        }
        return res;
    }

因为我们要的出某一列的水，就要知道该列左右各两边最高的之中的最低的一个有多低，但并不关心更高的哪一个有多高，所以，只要当右边有一个比左边最高的还高的时候就可以计算当前列的水了，让left在左边，right在右边，两个指针分别往中间靠，边靠边更新leftMax和rightMax，哪边比较小，就计算那边所对应的列，同时将对应的指针改变。

image-20240427191518934

2024-06-08 该篇文章被 jay1an 打上标签: 基础算法 双指针 归为分类: 基础算法

上一篇：滑动窗口 - Sliding Window 下一篇：哈希 - Hash
© 1949-2025 Jay1an
从头努力也坎坷 本站由Hexo驱动｜使用Hexo-theme-A4主题